This site presents a simple alternative approach to solve linear systems of inequalities with applications to optimization problems with continuous almost differentiable objective function with linear constraints. This class of optimization problems includes fractional, nonlinear network models, quadratic, and linear programs. This unified approach is accomplished by converting the constrained optimization problem to an unconstrained optimization problem through a parametric representation of its feasible region.
The proposed solution algorithm has nice features:
- It should prove useful for an introduction to mathematical programming before introducing more advanced topics.
- It is a general purpose solution algorithm, that is, one treatment for all linearly constraints optimization problems.
- Unlike other general purpose solution methods, such as KKT conditions, it guarantees global optimal solution.
- It is intuitively simple to be understood by non-mathematical major students and the managers.
- The prerequisite to understand the concepts, is minimal, it is assumed that the students are familiar with elementary calculus such finding the critical points of a given function.
- It provides useful information such all critical points which in turn, provides upper and lower tight bounds on the objective function over the feasible region.
- It provides useful managerial information such as sensitivity analysis and its applications to tolerance analysis.
- Since, there are many optimization problems with simply given postulated known solutions, the proposed solution algorithm is an effective tool for both, verifying the postulated known solution(s) or finding the best solution(s).
For illustrative and comparative purposes, the algorithm and its applications are presented in the context of numerical problems solved by other methods.
To search the site, try Edit | Find in page [Ctrl + f]. Enter a word or phrase in the dialogue box, e.g. "basic " or "linear " If the first appearance of the word/phrase is not what you are looking for, try Find Next.
MENU
- Introduction and Summary
- Identification of Vertices
- Parametric Representation
- Applications to Linear Programs
- Applications to Nonlinear Programs
- Optimal Business Decisions
- Optimization Over Unbounded Feasible Regions
- Post-optimality Analysis
- Concluding Remarks
- References
- JavaScript E-labs, Europe Mirror Site.
- Linear Optimization Solvers to Download (free-of-charge), Europe Mirror Site.
Companion Sites:
- JavaScript E-labs
- Linear Optimization Solvers to Download
- Success Science
- Leadership Decision Making
- Linear Programming (LP) and Goal-Seeking Strategy
- Artificial-variable Free LP Solution Algorithms
- Integer Optimization and the Network Models
- Tools for LP Modeling Validation
- The Classical Simplex Method
- Zero-Sum Games with Applications
- Computer-assisted Learning Concepts and Techniques
- Linear Algebra and LP Connections
- Construction of the Sensitivity Region for LP Models
- Zero Sagas in Four Dimensions
- Probabilistic Modeling
- Systems Simulation
- Business Keywords and Phrases
- Compendium of Web Site Review
- Collection of JavaScript E-labs Learning Objects
- Decision Science Resources
Introduction and Summary
Problem P: Maximize f(X)
Subject to:
| AX | £ | a |
| BX | ³ | b |
| DX | = | d |
with some variables Xj ³ 0, some Xj £ 0, and/or some Xj unrestricted in sign.
Matrices A, B, and D as well as vectors a, b, and d, have appropriate dimensions and f is an explicit continuous almost differentiable function. Problems like P belong to a subset of a larger set of problems known as Continuous Global Optimization Problems, with diverse areas of applications [see, e.g., Dravnieks and J. Chinneck (1997)].
Indeed, linearly constrained optimization problems are extremely varied. They differ in their functional form of the objective function, constraints, and in the number of variables. Although the structure of this problem is simple. Finding a global solution -- and even detecting a local solution is known to be difficult to solve. The simplest form of this problem is realized when the function f(X) is linear. The resulting model is a linear program (LP). Other problems include fractional, nonlinear network models, quadratic, separable, convex and nonconvex programs.
There are well over 400 different solution algorithms in solving different kinds of linearly constrained optimization problems. However, there is not one algorithm superior to others in all cases. For example in applying the Karush-Kuhn-Tucker (KKT) condition, it may be difficult, if not essentially impossible, to derive and optimal solution directly [see, e.g. Hillier and Lieberman (1995)]. The most promising numerical solution algorithm is the feasible direction method, however, if f is nonconvex then, the best one can hope for is that it converges to a local optimal point.
Since, there are many optimization problems with simply given postulated known solutions [see, e.g., Pardalos P., and Rosen J. (1987)], the proposed solution algorithm is an effective tool for both, verifying the postulated known solutions or finding the best solution(s).
The emerging field of global optimization deals with decision models, in the (possible) presence of multiple local optima with typically, the number of local pseudo-solutions is unknown, and it can be quite large. Furthermore, the quality of the various local and global solutions may differ significantly therefore global optimization problems can be extremely difficult to solve.
The classical numerical approaches lack a ‘universal’ and proven direct solver capability to tackle problems which possess multiple optima. In spite of the very significant theoretical advances in global optimization, software development and ‘standardized’ use lag behind. In this site we obtain global information for a class of problems in a complete and exhaustive fashion in developing a general solution algorithm that is robust.
In the proposed solution algorithm we need to find critical points. It is necessary for the domain to be an open set for the definition of derivative which is a limit with two sides (left and right limits). Therefore, we solve unconstrained problems over some relevant open sub-domains of the feasible region. First, we find critical points on the interior points of the feasible region. Next, we find critical points on interior points of the faces of the feasible region, then on interior points of the edges (i.e., line segments) of the feasible region. Finally, by functional evaluation of the objective function at the critical points and the vertices of the feasible region the global optimal solution is found. Therefore, in solving an n dimension problem, we solve some unconstrained optimization problems in n, n-1, ...., 1 dimensions. Thus, removing the constraints by the proposed algorithm reduces the constrained optimization to unconstrained problems which can be more easily dealt with.
The following provides an overview of the algorithm's process strategy:
Step 1: Find the feasible vertices and rays (if any).
Step 2: Find the interior critical points by using the gradient of the objective function and then select those which are interior by checking the constraints.
Step 3: Compute all other stationary points by first constructing the parametric representation of the objective function over the open domains of the faces, edges, and rays (if any), and then using its gradient, or by using the chain-rule for the construction the parametric gradient directly.
Step 4: Evaluate the objective function at critical points and vertices. Select the global solution.
Notice that we distinguish between stationary points and critical points. A critical point of a continuous function is a point where the first partial derivatives are zero or undefined. While "stationary point" is mostly used to mean a Kuhn-Tucker point. In an unconstrained problem it refers to the point where the gradient of the objective function is zero. Therefore, the set of stationary points is a subset of the critical point set for a continuous function. The roots of the for resultant nonlinear systems of equations can be find effectively by any efficient methods, such as the Newton's method referred to at Optimization with Sensitivity Analysis Resources Web site
The proposed algorithm requires continuous objective functions, however, it allows the possibility that the objective function being non-differentiable at a finite number of feasible points (i.e., almost differentiable). Because there are functions that are continuous everywhere without being differentiable at any point, see, e.g. Rudin (1976). A historical example (see, e.g., Townsend 1928, pp. 385-386) of a discontinuous derivative is:
There are specialized solution algorithms for the nondifferentiable optimization problems, see, e.g., Chen and Fukushima (1999), and Sherali, et al. (2000).
In the proposed solution algorithm we need to find critical points. It is necessary for the domain to be an open set to obtain the derivative which, is a limit with two sides (left and right limits). Therefore, we solve unconstrained problems over some relevant open sub-domains of the feasible region. These relevant domains are identified through a constraint-vertex table. First, we find the critical points on the interior of the feasible region. An interior point of the feasible region is a point that satisfies all the constraints but non-at the binding position. Next, we find the critical points on the faces of the feasible region, then on the edges of the feasible region. Finally, by evaluation of the objective function at critical points and vertices of the feasible region the global optimal solution is found. The removal of constraints in the proposed algorithm reduces the constrained optimization problem to some unconstrained optimization problems which can be easily dealt with using the gradient.
Another approach is to consider the subsets of polyhedron using simplicial decomposition, suggested in Von Hohenbalken (1977). However, the simplicial decomposition polyhedral feasible sets' algorithm is using Euclidean distances which are computationally tedious. Not much progress is made by the simplicial decomposition idea.
Identification of Vertices, Edges, and Faces
Geomerty of Polyhedra
Definition 1: A set S Î R n is a subspace of R n if every linear combination of points in S is also in S.
Definition 2: A point z Î R n is an affine combination of x and y if z = lx + (1 - l) y for some l Î R. (Note that we do not require 0 £ l £ 1.)
Definition 3: A set M is affine if every affine combination of points in M is also in M.
Definition 4: The points a 1, …… , a k are affinely independent if the vectors a 2 - a 1, a 3 - a 1, ......,a k - a 1 are linearly independent.
Definition 5: Given a scalar a and a vector a Î R n, the set { x | a T x ³ a} is a halfspace.
Definition 6: A polyhedron is a finite intersection of halfspaces. Note that the feasible region of a linear programming problem is a polyhedron.
Definition 7: The dimension of a subspace is the maximum number of linearly independent vectors in it.
Proposition 1 Every affine space is a translation of a subspace. Further, the subspace is uniquely defined by the affine space.
Definition 8: The dimension of an affine space is the dimension of the corresponding subspace.
Definition 9: The affine hull of a set is the set of all affine combinations of points in the set. This is equivalent to the intersection of all affine sets containing the set.
Definition 10: The dimension of a polyhedron is the dimension of its affine hull.
Definition 11: Let P be a polyhedron. Let H be the hyperplane H = { x | a T x = a. Let Q = P ÇH. If a T x ³ a for all x Î P then Q is a face of P.
Definition 12: Let P be a polyhedron of dimension d. A face of dimension d-1 is a facet. A face of dimension 1 is an edge. A face of dimension 0 is a vertex.
There are numerous effective and efficient solution algorithms for solving systems of linear equations with unrestricted variables in the linear algebra literature. These solution algorithms include pivoting, elimination, reduction, and triangularization methods, etc. [, see, e.g., Kelley (1995)]. However, the problem of solving a system of linear inequalities is much harder, and had to wait until era of the simplex method which solves linear programs (LP). By introducing a dummy objective function, the problem can be converted to a linear program and solved by LP algorithms to find one solution.
This section presents a direct method of solving a linear system of inequalities that does not require the formulation of an auxiliary LP problem and LP solution algorithms such as simplex. We provide a simple methodology to extend the solution of systems of inequalities of one or two dimensions to systems of higher dimensions. The proposed direct solution algorithm can be used in solving LP problems as an inverse approach. Under the proposed approach, the elaborate fundamental theorem of simplex method falls out as a by-product. Moreover, it can also be used to fill the gap between the graphical method of solving LP problems and the simplex method when teaching linear programming. We are interested in finding the vertices of the feasible region of problem P, expressed as system of linear equalities and inequalities
| AX | £ | a |
| BX | ³ | b |
| DX | = | d |
with some variables Xj ³ 0, some Xj £ 0, and some Xj unrestricted in sign.
Matrices A, B, and D as well as vectors a, b, and d, have appropriate dimensions. For ease and to conserve space, from now on, we refer to this general system of equalities-and-inequalities as "system" and its feasible region set as set S. Therefore, the optimization problem can be expressed as:
Problem P:
Max f(X)
subject to: X e S
2.1 Identification of Feasible Vertices:
The algorithmic strategy for finding all the vertices of the feasible region is as follows:
Construct the Boundaries of the Constraint Set: As pointed out earlier, if the objective function is nonlinear, the optimal solution to Problem P may be one of the stationary points on the interior, faces, edges, etc. of the feasible region in addition to the vertices. The interior of the feasible region is defined by the full set of the vertices obtained. Other relevant domains, such as faces, edges, etc. of the feasible region are defined by appropriate subsets of these vertices. Accordingly, we present the following method to identify all such subsets of vertices using a constraint-vertex table.
The coordinates of vertices are the basic feasible solution of the systems of equations obtained by setting some of the constraints at binding (i.e., equality) position. For a bounded feasible region, the number of vertices is at most combinatorial Cpq where p is the number of constraints and q is the number of variables. Therefore, by taking any q equations and solving them simultaneously one obtains a basic solution (if exists). By plugging this basic solution in the constraints of other equations, one can check for feasibility of the basic solution. If it is feasible, then this solution is a basic feasible solution that provides the coordinates of a corner point of the feasible region.
Definition 1: Each solution to any system of equations is called a Basic Solution (BS). Those Basic Solutions which are feasible are called Basic Feasible Solutions (BFS). The vertices of set S are the BFS.
Example 1: Suppose we wish to find the vertices of the following feasible region:
| 3X1 | + | 2X2 | £ | 6 | |
| X1 | ³ | 0, | X2 | ³ | 0. |
To illustrate the procedure, consider all of the constraints at binding position, i.e., all with equality (=) sign. This produces the following equations:
| 3X1 | + | 2X2 | = | 6 | X1 | = | 0 | X2 | = | 0 |
Here we have p=3 equations with q=2 unknowns. In terms of a "binomial coefficient", there are at most C32 = 3! / [2! (3-2)!] = 3 basic solutions. Solving the three resultant systems of equations, we have:
| X1 | X2 | Feasible? | |
| ------------------------- | |||
| 2 | 0 | Yes | |
| 0 | 3 | Yes | |
| 0 | 0 | Yes | |
Therefore the vertices of the feasible region are:
| X1=2 | X1=0 | X1=0 | ||
| X2=0 | X2=3 | X2=0 |
Example 2: Find the vertices of a set defined by the following system of inequalities:
| -3X1 | + | X2 | £ | 6 |
| X1 | + | 2X2 | £ | 4 |
| X2 | ³ | -3 |
Set all the constraints at their binding (i.e., equality) position. The result is the following set of 3 equations with 2 unknowns:
| -3X1 | + | X2 | = | 6 |
| X1 | + | 2X2 | = | 4 |
| X2 | = | -3 |
This gives the total number of possible basic solutions 3! / [(2!).(1!) = 3. We need to solve any two equations and then check the constraint of other for its feasibility. The result is summarized in the following table:
| X1 | X1 | Feasible? | |||
| ------------------------------------------------------- | |||||
| -8/7 | 18/7 | Yes | |||
| -3 | -3 | Yes | |||
| 10 | -3 | Yes | |||
The solutions in the above table are all the basic feasible solutions.Therefore, the vertices of the feasible region are:
| X1=-3 | X1=10 | X1=-8/7 | ||
| X2=-3 | X2=-3 | X2=18/7 |
For details and more numerical examples visit the Solution Algorithms for LP Models Web site.
Since we compute all the vertices of the feasible region, the proposed technique seems to be limited to small dimensions or very special domains. For example, for a cube in 10 dimensions we have already 1000 unconstrained variables. A more efficient method of finding all the vertices of a polytope is given in Arsham (1997a). Enumerating extreme points of highly degenerate polytopes are given in Yamada et. al. (1994). For an earlier work, see Altherr (1975). There is also a good directory of Codes for Polytope and Polyhedron Algorithms, which contains codes for generating all extreme points of a convex polyhedron given its system of linear inequalities.
2.2 Identification of Faces and Edges: As pointed out earlier, if the objective function is nonlinear, the optimal solution to Problem P may be one of the critical points on the interior of the faces, and edges/rays of the feasible region besides the vertices. Any point on a polytope is defined by the full set of the vertices obtained. Other relevant domains such as faces, edges, etc. of the feasible region are defined by appropriate subsets of these vertices. Accordingly, we present the following method to identify all such subsets of vertices using a constraint-vertex table.
Let n be the number of decision variables in the problem formulation. Construct a table with one column for each vertex and one row for each constraint including the sign-restriction conditions on the decision variables. Record in each cell of the table whether that vertex binds that constraint or not. First, obtain the sets of vertices that bind any one common constraint; each set so obtained defines a face in a three dimensional case and an edge in a two dimensional case. Next, obtain the sets of vertices that bind any two common constraints; each set so obtained defines an edge in the three dimensional case. Third, obtain sets of vertices that bind any three common constraints, and so on; but, not beyond (n-1) common constraints.
Consider the following feasible region:
X1 + X2 + X3 £ 10
3X1 + X3 £ 24
X1, X2, and X3 ³ 0.
The vertices, edges and faces of this feasible region is shown in the following figure.
Note that, in Figure 1, the feasible region is defined by a set of five constraints (which includes the three signed variables). The feasible region has six vertices, which can be found by the Algebraic Methods:
| X1 | X2 | X3 | FEASIBLE | |
|---|---|---|---|---|
| 0 | 0 | 0 | YES | |
| 0 | 0 | 10 | YES | |
| 0 | 0 | 24 | NO | |
| 10 | 0 | 0 | NO | |
| 8 | 0 | 0 | YES | |
| 8 | 2 | 0 | YES | |
| 0 | 10 | 0 | YES | |
| 0 | 10 | 0 | NO | |
| 7 | 0 | 3 | YES | |
| 0 | -14 | 24 | N0 |
Therefore, the vertices are the following points denoted by V1 through V6:
| X1 = 8 | X1 = 8 | X1 = 0 | X1 = 0 | X1 = 7 | X1 = 0 |
| X2 = 0 | X2 = 2 | X2 = 10 | X2 = 0 | X2 = 0 | X2 = 0 |
| X3 = 0 | X3 = 0 | X3 = 0 | X3 = 10 | X3 = 3 | X3 = 0 |
Therefore, there are a total of V = 6 vertices in our numerical example.
Construction of the Constraint-Vertex Table: In Figure 1, the feasible region is defined by a set of five constraints which includes the three sign-conditions on the decision variables. The feasible region has six vertices that represent the basic feasible solutions. The feasible region has five faces, nine edges and, of course, one interior set. Each vertex is uniquely defined by three constraints at binding position. Each face is defined by all vertices binding one common constraint. Each edge is defined by vertices binding two common constraints. All six vertices together define the feasible region.
| Constraints | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| X1+X2+X3£10 | no | yes | yes | yes | yes | no |
| 3X1 +X3£24 | yes | yes | no | no | yes | no |
| X1³0 | no | no | yes | yes | no | yes |
| X2³0 | yes | no | no | yes | yes | yes |
| X3=0 | yes | yes | yes | no | no | yes |
Face Identification: Finding the vertices which make one common constraint binding (i.e. faces of the feasible region):
| One Common Constraint | Vertices |
| X1+X2+X3£10 | 2,3,4,5 |
| 3X1+X3£24 | 1,2,5 |
| X1³0 | 3,4,6 |
Therefore, there are a total of F = 5 faces in our numerical example.
Edge Identification: Finding the vertices which make two common constraints binding (i.e., an edge of the feasible region)
| Two Common Constraints | Vertices |
| X1+X2+X3£10, 3X1+X3£24 | 2, 5 |
| X1+X2+X3£10, X1³0 | 3, 4 |
| X1+X2+X3£10, X2³0 | 4, 5 |
| X1+X2+X3£10, X3³0 | 2, 4 |
| 3X1+X3£24, X1³0 | No Edge |
| 3X1+X3£24, X2³0 | 1, 5 |
| 3X1+X3£24, X3³0 | 1, 2 |
| X1³0, X3³0 | 4, 6 |
| X1³0, X3³0 | 3, 6 |
| X2³0, X3³0 | 1, 6 |
Therefore, there are a total of E = 9 edges in our numerical example.
For any polyhedron in any dimensional space, let F be the number of faces, V the number of vertices, and E the number of edges, then there is always a linear dependency among these three characteristics, namely:
Parametric Representation
In this section, we represent a given linearly bounded feasible regions with finite number of vertices as a convex combination of its vertices. This representation allows us to convert a constrained problem into an unconstrained problem.
Generation of Feasible Local Optimal Solutions: Since the global optimal solution is one of the local optimal solutions. The global solution could be an interior point, a point of the faces of the feasible region or one of the vertices. The following figure depicts a typical example of a feasible region where the linear boundary lines (segments) define the feasible region marked by the gray area:
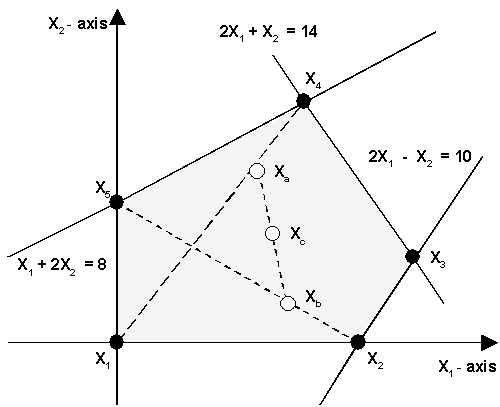
Generation
of Solutions in the Interior of the Feasible Region
Click on the image to enlarge it and THEN print it
To generate feasible solutions, the algorithm presented earlier generates the extreme points labeled by the black dots. The amount of extreme points can be very large, depending on the number of constraints and variable in the given instance.
These extreme points are fundamental in generating all the possible solutions. For example, interior feasible solutions Xa, Xb , and Xc, can be generated from the extreme points X1, X2, X4 and X5. For instance, Xa, is generated by the convex combination Xa = aa X1 + (1 - aa)X4 (with 0 £ aa £ 1). Similarly Xb = ab X2 + (1 - ab)X5 (with 0 £ ab £ 1). Finally, Xc is generated by the convex combination Xc = ac Xa + (1 - ac)Xb (with 0 £ ac £ 1). In conclusion, the whole feasible region can be generated by successive convex combination that can be traced to the extreme points, X1, X2, X3, X4 and X5.
Parametric Representation: Let us associate a parametric variable li for vertex Vi. Accordingly, for our previous example shown in figure 1, we have six variables, one associated with each of the six vertices. Any point feasible point can be represented as a convex combination of these six l's variables such that the sum of the values of all l's equals to 1; and, the value of each l is greater than zero and less than 1. Similarly, any point on a face of the feasible region can be represented as a convex combination of the l's associated with the vertices defining the face such that the sum of their values equals to 1; and, the value of each l is greater than zero and less than 1. Again, any point on the edge of the cube can be represented as a convex combination of the l's associated with the vertices defining the edge such that the sum of their values equals to 1; and, the value of each l is greater than zero and less than 1. Finally, of course, each vertex is defined by setting its associated l value to 1 and all other l's to zeros. The following formalized these discussions:
Definition 2: A convex combination of vertices V1, V2, ...., Vm is the set { Sli Vi : li ³ 0 and Sli = 1 for all i =1, 2, ...., m}.
Definition 3: The line segment connecting two adjacent vertices Vi and Vj of the feasible region is the set of points { l Vi + (1- l)Vj, 0 £ l £ 1}.
Definition 4: A polyhedron is the set that equals the intersection of a finite number of half-spaces. This is generally written as {X: HX £ h}, where the matrix H, and vectors X and h have appropriate dimensions.
Lemma 1: The set of all points defined by the system of equalities and inequalities.
| AX | £ | a |
| BX | ³ | b |
| DX | = | d |
with some variables Xj ³ 0, some Xj £ 0, and some Xj unrestricted in sign.
Definition 5: A polytope is a bounded polyhedron.
Lemma 2: If the feasible region is a polytope, then it can be represented as a convex combination; i.e., a Convex Hull, of its vertices.
Proof: The proof follows from the fact that polyhedra are convex and the boundedness of the set.
Example 3: Represent the feasible region defined by the following system of inequalities in parametric form:
| -3X1 | + | X2 | £ | 6 |
| X1 | + | 2X2 | £ | 4 |
| X2 | ³ | -3 |
This is a continuation of numerical example 2. As computed earlier, the vertices of the feasible region are:
| X1=-3 | X1=10 | X1=-8/7 | ||
| X2=-3 | X2=-3 | X2=18/7 |
The parametric representation of the feasible region with parameters l1, l2, and l3 for the first, second and third vertex, respectively, is:
| X1 | = | -3l1 | + | 10l2 | - | 8/7l3 |
| X2 | = | -3l1 | - | 3l2 | + | 18/7l3 |
for all parameters l1, l2, and l3 such that l1, l2, l3 ³ 0, and l1 + l2 + l3 = 1. This representation is also known as the Convex Hull of the feasible region. By substituting suitable values for these in the convex hull, one can generates any point of the feasible region.
In the following section we are using parametric representation to solve linear programs.
Applications to Linear Programs
Example 4: The following LP problem is from Hillier and Lieberman (1995, page 147):
| Max | -X1 | + | 4X2 | ||
| subject to: | -3X1 | + | X2 | £ | 6 |
| X1 | + | 2X2 | £ | 4 | |
| X2 | ³ | -3 | |||
| X1 | , | X2 | are unrestricted in sign |
As we found earlier, the vertices of the feasible region are:
| X1=-3 | X1=10 | X1=-8/7 | ||
| X2=-3 | X2=-3 | X2=18/7 |
The parametric representation of the feasible region is:
| X1 | = | -3l1 | + | 10l2 | - | 8/7l3 |
| X2 | = | -3l1 | - | 3l2 | + | 18/7l3 |
Substituting the parametric version of the feasible region into the objective function, we obtain:
f(l) = -X1 + 4X2 = -9 l1 - 22l2 + 80/7l3,
over the closed domain l1, l2, l3 ³ 0, and l1 + l2 + l3 = 1. This is a convex combination of three points on the real line R1; namely the coefficients -9, -22, and 80/7. Clearly, the optimal solution occurs when l3 = 1, and all other l's are set to 0, with maximum value of 80/7. Therefore, the optimal solution is X1 = -8/7, X2 = 18/7. Notice that the optimal solution is one of the vertices.
The following provides a generalization of the above results that the optimal solution of a bounded linear program occurs at a vertex of the feasible region S.
Proposition 2: The maximum (minimum) points of an LP with a bounded feasible region correspond to the maximization (minimization) of the parametric objective function f (l).
Let the terms with the largest (smallest) coefficients in f (l) be denoted by lL and lS respectively. Since f (l) is a (linear) convex combination of its coefficients, the optimal solution of f (l) is obtained by setting L or S equal to 1 and all other li = 0.
Lemma 3: The maximum and minimum points of an LP with a bounded feasible region correspond to lL = 1 and lS = 1, respectively.
This is a new proof of the well-known fundamental result in the simplex algorithm.
If a polytope has a finite number of vertices, then this result suggests that the optimal solution to an LP problem can be found by enumerating all possible basic feasible solutions found by the proposed solution algorithm. The optimum is associated with the basic feasible solution yielding the largest or smallest objective value, assuming the problem is of a maximization or a minimization type, respectively. The following example illustrates the process.
Example 5: The following problem is from Hillier and Lieberman (1995, page 143), which is solved therein by introducing first "artificial variables" needed to initialize the Simplex method, Arsham (1997b).
The proposed solution method is free from any extraneous elements which do not provide any useful information to the decision maker (the owner of the LP model), such as:
- artificial variables, used in initialization of the Simplex iterations,
- artificial constraints, used in the Dual Simplex method to satisfy the optimality condition,
- artificial objective function, used in the two-phase Simplex method, to generate a feasible vertex.
- extra variable(s) to convert any unrestricted variables to satisfy to non-negativity condition, such a condition is needed in the ordinary Simplex method.
| Max | 2X1 | + | 4X2 | + | 3X3 | ||
| subject to: | X1 | + | 3X2 | + | 2X3 | = | 20 |
| X1 | + | 5X2 | ³ | 10 | |||
| X1 | ³ | 0 | |||||
| X2 | ³ | 0 | |||||
| X3 | ³ | 0 |
Because the equality constraint X1 + X2 + X3 = 20, having positive coefficients of non-negative variables, the feasible region for this problem is bounded. Therefore , it suffices to evaluate the objective function at the feasible vertices. The coordinates of the vertices using the algebraic method, are tabulated in the following table.
Evaluation of objective function at the vertices of the feasible region:
| X1 | X2 | X3 | Feasible? | f(X) |
| ------------------------------------------ | ||||
| 0 | 0 | 10 | No | --- |
| 0 | 20/3 | 0 | Yes | 80/3 |
| 0 | 2 | 7 | Yes | 29 |
| 20 | 0 | 0 | Yes | 40 |
| 10 | 0 | 5 | Yes | 35 |
| 35 | -5 | 0 | No | --- |
Therefore the optimal solution occurs at X1 = 20, X2 = 0, X3 = 0, yielding an optimal value of 40.
Notice that if the feasible region is unbounded, then one must also use the rays of the feasible region, which will be constructed in Section 6.
Applications to Nonlinear Programs
Unlike linear programs, the optimal solution of nonlinear programs need not be a vertex of the feasible region. Although there exist general solution algorithms for linear programs, for non-linear programs more advanced solution algorithms are required. For example, the Lagrange Multiplier method [see, e.g., Fletcher (1987)], can be used to solve optimization problems with equality constraints and the Karush-Kuhn-Tucker approach [see, e.g., Fiacco and McCormick (1990), and Corradi (2001)] can be used to solve convex optimization problems. There are also special solution algorithms for special classes of problems, such as fractional and quadratic programs.
Upon representation of the feasible region and the objective function, we have:
Definition 6: critical points of a continuous function over an open set domain are the points where gradient vanishes, or it fails to exist.
Definition 7: A face of set S is a boundary set of S containing points on a line or plane (or hyper- plane). For example, in a two dimensional space, the faces are the boundary line segments between any two adjacent vertices.
Multivariable Unconstrained Optimization: To compute the global optimal point for problem P, we utilize the following necessary and sufficient procedure:
- Evaluate f(l) at its critical points within the feasible region.
- Evaluate f(l) at its critical points over the faces, and edges of the feasible region.
- Evaluate f(l) at the vertices of the feasible region.
- Select the maximum of the values obtained in steps 1, 2, and 3 to obtain the optimal solution to problem P.
Notice that it is an easier task to simply determine f(l) at all critical points and find the largest or smallest value, rather than using the second derivative (or the Hessian) to classify these critical points, as are shown in the following one-dimensional function f(l):
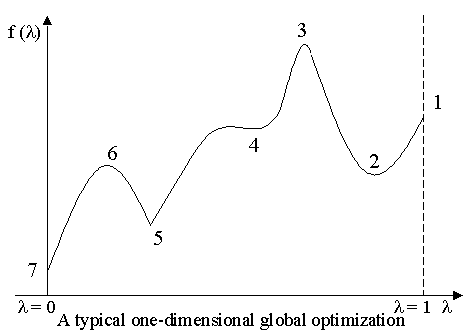
The above graph illustrates a typical one-dimensional global optimization problem. In Step 3, f(l) is evaluated at the boundary points, points 1 and 7, in the above graph. In Step 2, all critical points using the derivative (or the gradient) of f(l) are determined. For the above graph, Step 2 would detect the local critical at points 2, 3, and 6, as well as the inflection point of f(l) at point 4, and point 5 where derivative is not defined. It is an easier task to simply determine f(l) at all zero points of the gradient and find the largest (smallest, for the minimization problems) value, rather than using the second derivative (or the Hessian) to classify these points. Step 4 evaluates f(l) at all zero points of the derivative (or the gradient), as well as, the boundary points to determine the maximum (minimum) value of f(l). For the above function, the maximum value would be found at point 3 and the minimum value at point 7.
Now we state the following result based on the above procedure.
Proposition 2: If problem P has an optimal solution, then f(l) has a global solution.
In the following examples, we demonstrate how the proposed solution algorithm can be used to solve general non-linear programs over polytope S. The general problem is partitioned into a sequence of unconstrained sub-problems, each of which is handled by finding the critical points using the gradient. The stationary points are find by setting the gradients to zero, resulting in a system of equations which can be solved by the existing efficient methods, see, e.g., Ibidapo-Obe et al. (2002).
Example 6: The following nonlinear program with a logarithmic (Ln) term problem is from Hillier and Lieberman (1995, pages 583-585) which is solved therein by applying the Karush-Kuhn-Tucker optimality conditions.
| Max | f(X) = | Ln(X1+1) | + | X2 | |||
| subject to: | 2X1 | + | X2 | £ | 3 | ||
| X1 | ³ | 0, | X2 | ³ | 0 |
Step 1: Finding the Vertices of the Feasible Region:
The vertices of the feasible region are the points V1, V2, and V3, as shown below, respectively:
| X1=3/2 | X1=0 | X1=0 | ||
| X2=0 | X2=3 | X2=0 |
The gradient of the objective function is: Ñ f(X) = [1/(X1 + 1), 1] which does not vanish, and it is undefined at X1 = -1 which is not feasible. Therefore, there is no any interior critical point for this problem.
Step 3: Finding the critical Points on the Boundary Line Segments:
The line segment joining the following two adjacent vertices:
| X1=3/2 | X1=0 | |
| X2=0 | X2=3 |
can be represented as a parametric form using the convex combination of the adjacent vertices:
| X1 | = | 3/2l1 | ||
| X2 | = | 3l2 | = | 3-3l1 |
The derivative of f(X) with respect to l1 is:
f ‘ ( l1) = å ¶ f(X) / ¶Xi . ¶Xi / ¶ l1 = [1/(X1 + 1)](3/2)] + [1](-3)] = (-4.5 l1 -1.5)/ (1.5l1 +1) which is negative.
Similarly, finding the critical points on the boundary line segment joining the two adjacent vertices:
| X1=3/2 | X1=0 | |
| X2=0 | X2=0 |
The parametric representation of the line segment is:
| X1 | = | 3/2l1 |
| X2 | = | 0 |
The derivative f ‘ ( l1) = [1/(X1 + 1)](3/2)] + [1](0)] = 1.5 / (1.5 l1 + 1) which is positive.
Finding the critical points on the boundary line segment joining the two adjacent vertices:
| X1=0 | X1=0 | |
| X2=3 | X2=0 |
The parametric representation of the line segment is:
| X1 | = | 0 |
| X2 | = | 3l1 |
The derivative f ‘ ( l1) = [1/(X1 + 1)](0)] + [1](3)] = 3 which is positive.
Step 4: Evaluation of Objective Function at the Vertices of the Feasible Region:
| l1 | l2 | l3 | f(l) |
| ----------------------------------- | |||
| 1 | 0 | 0 | Ln(1.5) |
| 0 | 1 | 0 | 3 |
| 0 | 0 | 1 | 0 |
Therefore the optimal solution occurs at l1 = 0, l2 = 1, l3 = 0, which is the vertex X1 = 0, X2 = 3, yielding an optimal value of 3.
Example 7: The following quadratic program is from Hillier and Lieberman (1995, pages 586-591) which is solved therein by the Modified Simplex Method.
| Max | f(X) = | 15X1+30X2+4X1X2-2X12-4X22 |
| subject to: | X1+2X2£ 30 | |
| X1³ 0, X2³ 0 |
Step 1: Finding the Vertices of the Feasible Region:
By applying the algebraic method, the vertices of the feasible region are:
| X1=30 | X1=0 | X1=0 | ||
| X2=0 | X2=15 | X2=0 |
Step 2: Computation of the Interior critical Points:
The gradient of the objective function is: Ñ f(X) = [15 + 4X2 - 4X1, 30 + 3X1 -8X2] which vanishes at (X1 = 15, X2 = 45/4) which is not feasible. Therefore, there is no any interior critical point for this problem.
Step 3: Finding the critical Points on the Boundary Line Segments:
To find the critical points of the line segment joining the following two vertices,
| X1=30 | X1=0 | |
| X2=0 | X2=15 |
first we represent a parametric form of the line segment using the convex combination of the adjacent vertices. That is:
X1 = 30l1
X2 = 15l2 = 15 - 15 l1
over the open set 0 < l1 < 1
The derivative of f(X) with respect to l1 is:
f ‘ (l1) = å ¶ f(X) / ¶Xi . ¶Xi / ¶l1 = (15 + 4X2 - 4X1)(30) + (30 + 3X1 -8X2)(-15) = -1200 l1 + 480.
The derivative vanishes at l1 = 2/5. This corresponds to the critical point (X1 = 12, X2 = 9) with f(X) = 540.
Similarly, for the boundary line segment between the following two vertices:
| X1=30 | X1=0 | |
| X2=0 | X2=0 |
first we represent a parametric form of the line segment using the convex combination of the adjacent vertices. That is:
X1 = 30l1
X2 = 0
over the open set 0 < l1 < 1
The derivative of f(X) with respect to l1 is:
f ‘ (l1) = å ¶ f(X) / ¶Xi . ¶Xi / ¶l1 = (15 + 4X2 - 4X1)(30) = -3600 l1 + 450.
The derivative vanishes at l1 = 1/8. This corresponds to the critical point (X1 = 15/4, X2 = 0) with f(X) = 28.125.
Finally, for the boundary line segment between the following two vertices:
| X1=0 | X1=0 | |
| X2=15 | X2=0 |
first we represent a parametric form of the line segment using the convex combination of the adjacent vertices. That is:
X1 = 0
X2 = 15l1
over the open set 0 < l1 < 1
The derivative of f(X) with respect to l1 is:
f ‘ (l1) = å ¶ f(X) / ¶Xi . ¶Xi / ¶l1 = (30 + 4X1 -8X2)(15) = -1800 l1 + 450.
The derivative vanishes at l1 = 1/4. This corresponds to the critical point (X1 = 0, X2 = 15/4) with f(X) = 56.25.
Step 4: Evaluation of Objective Function at the Vertices of the Feasible Region:
| l1 | l2 | l3 | f(l) |
| ---------------------------------- | |||
| 1 | 0 | 0 | -1350 |
| 0 | 1 | 0 | -450 |
| 0 | 0 | 1 | 0 |
Now, comparing all the functional valuations, the optimal solution has l1 = 2/5, l2 = 3/5, l3 = 0. This gives X1 = 12, X2 = 9 yielding an optimal value of 540.
Example 8: The following problem is from Hillier and Lieberman (pages 600-603) which is solved therein by applying the Frank-Wolfe Algorithm.
| Max | f(X) = | 5X1 | - | X12 | + | 8X2 | - | 2X22 |
| subject to: | 3X1 | + | 2X2 | £ | 6 | |||
| X1 | ³ | 0, | X2 | ³ | 0 |
Step 1: Finding the Vertices of the Feasible Region:
The vertices of the feasible region are:
| X1=2 | X1=0 | X1=0 | ||
| X2=0 | X2=3 | X2=0 |
Step 2: Computation of the Interior critical Points:
The gradient of the objective function is: Ñ f(X) = (5 - 2X1, 8 - 4X2) which vanishes at (X1 = 5/2, X2 = 2) which is not feasible. Therefore, there is no any interior critical point for this problem.
Step 3: Finding the critical Points on the Boundary Line Segments:
To find the critical points of the line segment joining the following two vertices,
| X1=2 | X1=0 | |
| X2=0 | X2=3 |
first we represent a parametric form of the line segment using the convex combination of the adjacent vertices. That is:
| X1=2l1 | |
| X2= 3l2 = 3 - 3l1 |
The derivative of f(X) with respect to l1 is:
f ‘ (l1) = å ¶ f(X) / ¶Xi . ¶Xi / ¶l1 = (5 - 2X1)(2) = (8 - 4X2)(-3) = 22 -44l1
The derivative vanishes at l1 = 1/2, which corresponds to the critical point (X1 = 1, X2 = 3/2), with f(X) = 11.5.
Similarly, to find the critical points of the line segment joining the following two vertices,
| X1=2 | X1=0 | |
| X2=0 | X2=0 |
first we represent a parametric form of the line segment using the convex combination of the adjacent vertices. That is:
| X1=2l1 | |
| X2=0 |
The derivative of f(X) with respect to l1 is:
f ‘ (l1) = å ¶ f(X) / ¶Xi . ¶Xi / ¶l1 = (5 - 2X1)(2) = 10 - 8l1
which has a critical point at l1 = 5/4 which is not feasible.
Finally, to find the critical points of the line segment joining the following two vertices,
| X1=0 | X1=0 | |
| X2=3 | X2=0 |
first we represent a parametric form of the line segment using the convex combination of the adjacent vertices. That is:
| X1=0 | |
| X2=3l1 |
The derivative of f(X) with respect to l1 is:
f ‘ (l1) = å ¶ f(X) / ¶Xi . ¶Xi / ¶l1 = (8 - 4X2)(3) = 24 - 36l1
The derivative vanishes at l1 = 2/3, which corresponds to the critical point (X1 = 0, X2 = 2), with f(X) = 8.
Step 4: Evaluation of Objective Function at the Vertices of the Feasible Region:
| l1 | l2 | l3 | f(l) |
| ------------------------------------ | |||
| 1 | 0 | 0 | 4 |
| 0 | 1 | 0 | 6 |
| 0 | 0 | 1 | 0 |
Now, comparing all the functional valuations, the optimal solution has l1 = 1/2, l2 = 1/2, and l3 = 0. This gives X1 = 1, X2 = 3/2 with an optimal value of 10.5.
Optimal Business Decisions
From the manager’s perspective, a better understanding of optimization techniques would prove most helpful in arriving at well-reasoned decisions. Unfortunately, even though most managers and business students have the basic calculus skills necessary to understand and learn such techniques, training in optimization theory is receiving little attention.
Current State of Optimization Applications in Business
Almost all finance textbooks avoids the complexities of the allocation problem entirely, and use pictorial approaches to explain how the frontier of efficient investment portfolios can be constructed. By plotting the expected returns of all possible portfolios in relation to their respective variances, and by drawing an envelope around the portfolios that has the largest return for any level of variance. Doing so, a graph emerges that depicts the portfolios that generate the greatest expected return for any given level of variance. Although this approach describes the nature of the problem, the investor’s choice of portfolio weights remains a second-stage decision. What is not pointed out is that the investor would need to compute the returns and variances of an infinite number of portfolios to implement this approach. Even if the decision-maker is able to construct the frontier using this pictorial approach, the actual selection process requires the additional step of constructing a map of the investor’s indifference curves and finding a tangency between the indifference curves and the efficient set of portfolios. Furthermore, the challenges presented in constructing the indifference map are non-trivial.
A critical assessment of the more advanced textbooks reveals that most of the mathematical details provided are relegated to appendices. For the most part, the explanations offered are prohibitively complex, difficult to understand, computationally tedious, generally just descriptive in nature, and often provide more questions than answers. More troubling is that even with a higher level of mathematical content, key components of the approaches may be omitted on the grounds that they are beyond the scope of the textbook. As an example, Elton et al (2003) outline the critical-line approach to solving the investment problem. This algorithm requires the determination of corner points at which the objective function changes direction, but there is no explanation as to how these corner points are determined. The authors provide interested readers with a reference that explains how to find the corner points, but without the corner points the algorithm cannot be implemented. In a similar fashion, Sharpe et al (1999) claim that the critical-line method is beyond the scope of the book.
It may be feasible for students to learn how to apply Karush-Kuhn-Tucker (KKT) conditions to solve problems of this type, but the necessary knowledge to do so correctly –in particular, to recognize when the conditions are violated– may be challenging. Elton et al. (2003) provide examples that apply KKT conditions, but, without a substantial amount of effort, the students’ level of understanding is unlikely to be enhanced, and in any case, the approach is quite laborious.
Taking all of the existing textbooks together, they still fail to provide easy to implement decision-making tools and do little to advance the intuition underlying constrained optimization problems. This is most unsatisfactory indeed. The end result is that the current textbook treatment does not provide students with an approachable means of mastering this important and useful topic. This trend is unfortunate because decision-making skills and intuition can be greatly improved at relatively low intellectual cost.
We consider the manager’s primary objective is a methodology that provides a prescriptive, rather than a purely descriptive, solution. To make this workable, it is crucial to provide an explanation that is simpler to teach and understand, that will enhance the reader’s ability to make better decisions, and that will provide the intuition necessary to understand complex optimization problems. The key to addressing this problem is to provide a simple and easily implemented algorithm that requires little mathematical sophistication. Once a decision-maker has mastered this approach, he or she will have a far better understanding of optimization problems in general, and this will allow them to evaluate more adequately any proposed solutions presented by better-trained analysts or other consultants. It is possible to provide a bridge between an analyst with a high level of mathematical training and a manager faced with the difficulty of making the final decision.
This part of the site presents a simple algorithm for determining the globally optimal solution to linearly constrained optimization problems. It requires only the most basic mathematical skills; so, it is approachable by a wide range of business students. Obvious applications include portfolio selection, economics, marketing, and production problems. The algorithm will prove useful also as an introduction to optimization prior to introducing more advanced topics.
The proposed algorithm relies on evaluation of the objective function. The need to compute the Hessian is eliminated. Consequently, managers and students who are not mathematics majors easily understand it. The only prerequisite is an understanding of the basic calculus needed to find critical points of a function. In addition to its overall simplicity, the algorithm has several other attractive features. It is a general-purpose approach applicable to all linearly constrained optimization problems. And, unlike other methods, such as the KKT conditions, it guarantees that the solution is globally optimal. The algorithm also provides useful information such as all of the critical points of the objective function that in turn, provide tight upper and lower bounds over the feasible region.
In the proposed solution algorithm, we need to find critical points. Notice that we distinguish between stationary points and critical points. A critical point of a continuous function is any point where the first partial derivatives are zero or undefined, while stationary point is generally used to mean a KKT point. In an unconstrained problem, a stationary point refers to the point where the gradient of the objective function is zero. Therefore, the set of stationary points is a subset of the critical points set for a continuous function.
The following provides an overview of the solution strategy:
- Find the interior critical points by using the gradient of the objective function, and then select those that are feasible by checking the constraints.
- Find vertices of the feasible region. Arsham (1997) provides a simple and direct algebraic methodology for solving a linear system of inequalities by finding vertices of the feasible region without using slack/surplus variables.
- Compute all other critical points first by constructing the parametric representation of the objective function over the open domains of the boundaries of the feasible region, and then by using its gradient, or by using directly the chain?rule for the construction of the parametric gradient.
- Evaluate the objective function at critical points and vertices.
- Select the global solution (if any).
Since we employed a convex parametric transformation, therefore, if the problem has a global optimal solution, then f(l) has a global optimal solution. The following steps summarize the implementation of the proposed solution algorithm:
Step 1. Evaluate f(l) at its stationary points within the interior of the feasible region.
Step 2. Evaluate f(l) at its stationary points within the interior of the faces and edges of the feasible region identified in the constraint-vertex table.
Step 3. Evaluate f(l) at the vertices of the feasible region.
Step 4. Select the global optimal solution(s).
Notice that it is easier to evaluate simply f(l) at all stationary points and at the vertices and to select the largest or the smallest value, depending on whether the problem is of maximization or minimization type. Such an approach is much simpler than employing the needed the second order derivatives of f(l) or its Hessian, in deciding whether a given stationary point is a maximum or a minimum point.
Since the gradient is defined over an open set, we eliminate one of the appropriate l by utilizing the fact that Sli’s = 1 in making the domain an open set. Therefore, we solve unconstrained problems over some relevant open sub-domains of the feasible region. First, we find the critical points on the interior of the feasible region. An interior point of the feasible region is a point that satisfies all of the constraints, but the constraints are non?binding at that point. Next, we find the critical points on the boundaries of the feasible region. Finally, evaluation of the objective function at critical points and vertices of the feasible region provides the global optimal solution. The removal of constraints in the proposed algorithm reduces the constrained optimization problem to some unconstrained optimization problems, which can be easily dealt with using the gradient.
Applications to Optimal Business Decisions
Optimization is at the core of rational decision making in business. Even when the decision-maker has more than one goal, or when there is significant uncertainty in the system, optimization provides a rational framework for efficient decisions. The Markowitz mean-variance formulation is a classic example. This section illustrates the solution algorithm and its applications to finance, economics, marketing, and production in the context of numerical examples already solved by other methods.
Financial Applications: Although there are a variety of portfolio selection models, the widely used method is its formulation as a quadratic optimization problem.
The following portfolio selection is from Haugen (1997) that is solved by Karush-Kuhn?Tucker conditions, which assumes that the objective function is convex.
As in Haugen (1997), we will use the quadratic performance measure as a minimization of risk:
Min f(X) =
Clearly, the objective function and equality conditions indicate this is a continuous optimization problem with a bounded feasible region. We now follow the algorithmic steps outlined earlier.
Step 1: For this three-dimensional decision-variable problem, the feasible region is the line segment joining the following two vertices: A=(0, 1, 0), and B=(1/2, 0, 1/2), with f(A) = f(0, 1, 0) = 0.21 and f(B)= f(1/2, 0, 1/2) = 0.215
Step 2: Find the critical points on the line segment: The parametric representation of the line segment AB is:
| X1 = 0l1 + 1/2l2 = 1/2l2 |
| X2 = 1l1 + 0l2 = 1 - l2 |
| X3 = 0l1 + 1/2l2 = 1/2l2 |
over the open set 0 < l2< 1
Using the chain-rule, the derivative of f(l) with respect to l2 is:
f ‘ (l2) = å ¶ f(X) / ¶Xi . ¶Xi / ¶l2 =
(0.5X1 + 0.3X2 + 0.34X3)(1/2) +
(0.42X2 + 0.3X1 + 0.18X3)(-1) +
(0.56X3 + 0.34X1 + 0.18X2)(1/2)
=
0.75l2 – 0.36
The derivative vanishes at
l2 = 12/25. This gives an interior critical point C1 = (X1 = 1/2l2 = 0.24, X2 = 1- l2 = 0/52, X3 = 1/2l2 = 0.24) with objective values of 0.1668
Step 3: There is no edge for this problem.
Step 4: Now by comparing the numerical values of f(X) at vertices and point C1, we conclude that the optimal solution is at point C1 = (0.24, 0/52, 0.24) with optimal value 0.1668 . By having the above information, one readily constructs the numerical tight bounds for the objective function, that is,
0.1668 £ 0.2X12 + 0.21X22 + 0.28X32 + 0.3X1X2 + 0.34X1X3 + 0.18X2X3 £ 0.215, over its feasible region.
A Non-Convex Quadratic Optimization: Now suppose the covariance 0.34 is negative, say -0.5. The problem is:
Notice that the KKT condition-set does not provide any solution to this non-convex problem. However, with the new approach, we will follow the same steps as before.
| X1 = 0l1 + 1/2l2 = 1/2l2 |
| X2 = 1l1 + 0l2 = 1 - l2 |
| X3 = 0l1 + 1/2l2 = 1/2l2 |
over the open set 0 £ l2£ 1
Using the chain-rule, the derivative of f(l2) with respect to l2 is:
f ‘ (l2) = å ¶ f(X) / ¶Xi . ¶Xi / ¶l2 =
(0.5X1 + 0.3X2 – 0.5X3)(1/2) +
(0.42X2 + 0.3X1 + 0.18X3)(-1) +
(0.56X3 - 0.5X1 + 0.18X2)(1/2)
=
0.045l2 + 0.18
The derivative does not vanish. Therefore there is no interior stationary point for this problem. Step 4: Comparing the numerical values of f(X) at two vertices: A=(0, 1, 0), B=(1/2, 0, 1/2), with f(A)= 0.21, and f(B)= 0.01.
We conclude that the optimal solution is at point B = (1/2, 0, 1/2) with optimal value 0.01. By having the above information, one readily constructs the numerical tight bounds for the objective function, that is,
0.01 £ 0.2X12 + 0.21X22 + 0.28X32 + 0.3X1X2 - 0.5X1X3 + 0.18X2X3 £ 0.21, over its feasible region.
Economics Applications: The following Micro-Economics optimization with a logarithmic utility objective function is from Kreps (1990, pages 778-782) which is solved therein by applying the Karush-Kuhn-Tucker conditions. The problem involves maximizing the utility due to consumption of two products, wheat and corn. No more than $10 can be spent for the purchase of these products and the total caloric content may exceed 1500. The decision variables are: X1 = number of units of wheat, and X2 = number of units of candy.
| Max | f(X) = | 3log(X1) | + | 2log(2 + X2) | |||
| subject to: | X1 | + | X2 | £ | 10 | ||
| 150X1 | + | 200X2 | £ | 1500 | |||
| X1 | ³ | 0, | X2 | ³ | 0 |
In solving this problem, we follow the algorithmic steps outlined earlier.
Step 1: The graph of the feasible region provides the vertices, which are A, B, C, and D, respectively:
| X1 = 10 | X1 = 9 | X1 = 0 | X1 = 0 | |||
| X2 = 0 | X2 = 1 | X2 = 31/9 | X2 = 0 |
| X1 | = | 10l1 | + | 9l2 |
| X2 | = | l2 | + | 31/4l3 |
Step 2:The parametric representation of the interior points of the feasible region is:
The parametric objective function (after the substitutionl4 = 1 - l1 - l2 - l3 ) is:
f ( l) = 3log (10l1 + 9l2 ) + 2log(l2 + 31/4l3 + 2) Step 2: The gradient does not vanish anywhere therefore, there is no any interior stationary point.
Step 3: Representation of f(X) on the edge joining the following two vertices B and C:
| X1 = 9 | X1 = 0 | |
| X2 = 1 | X2 = 31/4 |
The parametric objective function (after substitution l2 = 1 - l1) is:
f (l1) = 3log (9l1) + 2log(39/4 – 27/4l1)
The derivative vanishes at ?1 = 13/15. Thereforel1 = 13/15, l2 = 2/15 which gives X1= 39/5, X2 = 19/10, with f(X) = 8.9. On the other remaining edges the derivatives do not vanish.
Step 4: Evaluation of objective function at the vertices of the feasible region: A=(10, 0), B=(9, 1), C=(0, 31/9), D=(0, 0), with f(A)= 3log10, f(B)= 3log9, f(C)= 3log(31/4), and f(D)= Undefined.
Therefore, the optimal solution occurs at X1= 39/5, and X2 = 19/10 with an optimal value of 8.9. By having the above information, one is able to provide only the numerical upper bound for the objective function, that is,
3log(X1) + 2log(2 + X2 £ 8.9, over its feasible region.
Marketing Applications: The following Marketing nonlinear (quadratic) programming problem is from Markland and Sweigart (1987, pages 719-720) which is solved therein by the Lagrangian multiplier method. The problem involves maximizing the sales of a product subject to the total $1000 available for marketing that must be spent on newspaper and/or radio commercials advertising campaign. The decision variables are: X1 = number of units of newspaper advertisements, and X2 = number of units of radio commercials.
We now follow the algorithm:
Step 1: The vertices of the feasible region are:
| X1 = 10/3 | X1 = 0 | |
| X2 = 0 | X2 = 5 |
The parametric representation of the interior of the feasible region is:
X1 = 10/3l1
X2 = 5l2 = 15 - 15 l1
over the open set 0 < l1 < 1
Step 2: The parametric objective function is:
f ( l) = -17500/3l12 + 20500l1 - 10000
The derivative of f(l) vanishes at l1 = 41/70. Therefore, l1 = 41/70, l = 29/70, and f(l) = 12000. This gives X1 = 41/21, and X2 = 29/14, with f(X) = 12000.
Step 3: Evaluation of objective function at the vertices of the feasible region: A=(10/3, 0), and B=(0, 5) with f(A)= 4000, and f(B)= 2400
Step 4: Therefore, the optimal solution occurs at X1= 41/21, and X2 = 29/14 with an optimal value of 12000. By having the above information, one readily constructs the numerical tight bounds for the objective function, that is,
2400 £ 4300X1 -300X12 + 2500X2 - 100X22 £ 12000, over its feasible region.
Production and Operation Management Applications: Many practical nonlinear mathematical programming leads to optimizing a quotient of two functions subject to a set of linear constraints. The areas of applications include, cutting stock problem to minimize the ratio of wastage to useful output, ship scheduling to maximize the ratio of profit per journey to total journey, and the Markov chain decisions of finding minimum cost policies for the management of stochastic systems. The following fractional optimization problem is from Chadha (1999) that is solved by a specialized solution algorithm therein.
Clearly, the non-negativity conditions indicate that the denominator of the objective function does not vanish within the feasible region; therefore, this is a continuous optimization problem with bounded feasible region. We now follow the algorithm:
Step 1: Since the feasible region is only a line segment, there are no interior critical points.
Step 2: Notice that, for this two-dimensional problem, the feasible region is the line segment joining the following two vertices: A=(3/2, 3/2), and B=(2, 2) with f(A)= 3, and f(B)= 16/5.
Step 3: Finding the critical points on the line segment: The parametric representation of the line segment AB is:
| X1 = 3/2l1 + 2l2 = 3/2l1 + 2(1 - l1) = 2 - l1/2 |
| X1 = 3/2l1 + 2l2 = 3/2l1 + 2(1 - l1) = 2 - l1/2 |
Therefore, the parametric representation of the problem over AB is:
Max f(l1) = (16 -4l1) / (5 - l1), for 0 < l1 < 1
The derivative of f(l1) is:
f ’(l1) = -4 /(5 - l1)2
which is always negative over its domain. Therefore, there is no critical point for this problem.
Step 4: Now by evaluating f(X) at vertices, we conclude that the optimal solution is at (2, 2) with an optimal value of 16/5. This solution is superior to the solution (X1, X2) = (3/2, 3/2), with objective value of 3, obtained in the above reference. By having the above information, one readily constructs the numerical tight bounds for the objective function, that is,
3 £ (2X1 + 6X2) / (X1 + X2 + 1) £ 16/5, over its feasible region.
Conclusions: A critical evaluation of the current literature on even local optimization solution algorithms with business applications reveals that their approaches are frequently too complex, computationally laborious, and difficult to implement. Finding the global solution for general optimization problems is not an easy task. This paper proposes an enumeration procedure to obtain the global solution to linearly constrained optimization problems with almost differentiable objective functions. The key to the general solution algorithm is the removal of constraints through parametric representation of the problem using the convex combination of the vertices of its feasible region. The vertices are obtained by a simple and direct algebraic method. Computing stationary points and evaluating the objective function at these points as well as at the vertices then find the globally optimal solution.
Optimization Over Unbounded Feasible Regions
Identification of Unbounded Polyhedral Region: Given the following standard-form feasible region F = { X: A X = b, X ³ 0}, where A is a given m by n matrix and b is a m-vector, we are interested to check if the feasible region is unbounded or not.
Lemma 4: Given the set F is nonempty then F is unbounded if and only if the following LP problem has a nonzero vector Y as its solution:
Maximize S Yi
Subject to: A Y = 0, 0 £ Yi £ 1, for all i’s
Proof follows from Farkas' lemma, see, e.g. Nocedal and Wright, (2006), or Boyd and Vandenberghe (2004) . Moreover, the optimal solution Y* will be an unbounded direction.
Notice that solving a simple LP with a dummy objective function, such as:
Minimize X1
Subject to: A X = b, X ³ 0
can check the condition that F must be nonempty, if this simple LP has a bounded solution.
We now employ a numerical example to illustrate the above procedure.
Consider the following nonempty feasible region:
| 5X1 | - | X2 | £ | 30 | |
| X1 | £ | 5 | |||
| X1 | ³ | 0 | , | X2 | is unrestricted in sign |
To convert the feasible region to the standard form can be achieved by substituting X2 – X3 for X2, and introducing slack variables X4, and X5 for the two £ constraints, respectively. The standard-form of the region is:
| 5X1 | - | X2 | + | X3 | + | X4 | = | 30 |
| X1 | + | X5 | = | 5 |
All variable are nonnegative.
The above feasible region is unbounded if and only if the following LP has a non-zero Y* as its optimal solution:
Maximize Y1 + Y2 + Y3 + Y4 + Y5
| 5Y1 | - | Y2 | + | Y3 | + | Y4 | = | 0 |
| Y1 | + | Y5 | = | 0 | ||||
| Yi | £ | 1 | , | for all i’s, |
and all variable are nonnegative.
The optimal solution is Y* = [0, 1, 1, 0, 0] which is nonzero. Therefore, the feasible region is indeed an unbounded one.
Definition 8: A ray is a half-line: {V + ah: a ³ 0}, where h is a non-zero vector of S. Point V is called the root, and it is said that the ray is rooted at V.
Definition 9: A extreme ray of a closed set S is a ray in S that cannot be expressed as a linear combination of other rays in S.
General idea for parametric representation is that we start at a vertex. We move away from it in the feasible direction of every edge to the next feasible point. If such point exists (i.e., we have found another vertex). If not, the polyhedron is not constrained in that direction and it means that the direction is an extreme ray. Notice that, the polyhedron without vertex always contains a line (or hyper-plane). For such polyhedron we also have to add additional ray perpendicular to that line (or hyper-plane) IF the constraint is in the form of inequality ( ³, or £. For more details read, e.g. Chvatal (1983), Ch. 8.
An Application: A polyhedron with some vertices can be expressed as convex combination of the vertices and parametric extreme rays, known in vector algebra as V-representation [see, e.g., Ziegler (1995)]. Therefore, for the nonlinear programs with closed unbounded feasible region we find the vertices and rays of the feasible region. At the next step we find the interior critical points using the gradient of the objective function. This is follows by finding the critical points on the faces, edges and rays via parametric representation of the objective function or using the chain-role for computing the gradients. Finally we evaluate the objective function at the vertices.
Note that, in step 2, in order to obtain any interior critical points, we first relax all constraints, and find the critical points of the objective function. An interior point of the feasible region is a point that satisfies all the constraints but non-at the binding position.
We now employ a numerical example to illustrate the above procedure.
Example 9: Consider the following problem:
| Min | f(X) = | X1 | - | X22 | + | 4 X2 | ||||
| subject to: | 5X1 | - | X2 | £ | 30 | |||||
| X1 | £ | 5 | ||||||||
| X1 | ³ | 0 | , | X2 | is unrestricted in sign |
Step 1: Finding the Vertices of the Feasible Region: The feasible region for this problem has two extreme rays which are rooted at its two vertices as shown by the following figure:
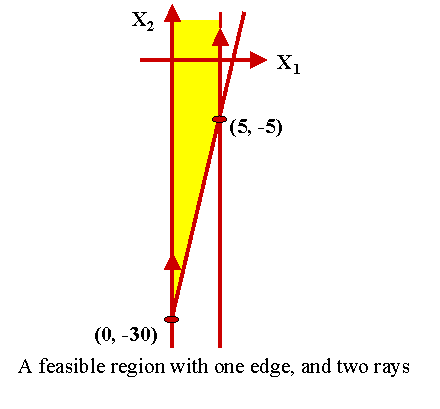
Step 2: Finding the Interior Critical Points: The gradient of the objective function is Ñ f(X) = (1, -2X2 + 4), which does not vanish. Therefore, there is no critical point in the interior of the feasible region.
The Parametric Version of the Feasible Region:
(X1, X2) = l1 . (0, -30) + l2 . (5, -5) + a . (0, 1),
for all l1³ 0, l2³ 0, l1 + l2 = 1, a³ 0.
Step 3: Finding the critical Points on the Boundary Line Segments and the Rays: To find the critical points of the line segment joining the following two vertices (0, -30) and (5, -5), first we represent a parametric form of the line segment using the convex combination of the adjacent vertices. That is:
X1 = 5 l1,
X2 = -5l1 - 30l2 = 25l1 - 30, for 0 < l1 < 1
The derivative of f(X) with respect to l1 is:
f ‘ (l1) = å ¶ f(X) / ¶Xi . ¶Xi / ¶l1 = (1)(5) + (-2X2 +4)(25) = -1250l1 + 1605 which is always positive. Therefore, there is no critical point on this line segment.
To find the critical points on the interior points of extreme ray rooted at (0, -30), in the direction of (0, 1), first construct a parametric version of extreme ray as:
(X1, X2) = (0, -30) + a(0, 1) = (0, -30 + a), for a > 0.
The derivative of f(X) with respect to a is:
f ‘ (a) = å ¶ f(X) / ¶Xi . ¶Xi / ¶a = 1(0) + (-2X2 + 4)(1) = 64 - 2a, for a > 0.
The derivative vanishes at a = 32, therefore a critical point is at (0, 2), with the objective function value of 4. Notice that since f'(a) is positive for any a > 32 , therefore the objective function is increasing beyond this point, hence, there is no global maximum point for this problem.
Similarly,to find the critical points on the interior points of extreme ray rooted at vertex (5, -5), in the direction of (0, 1), construct the parametric version of its interior points as:
(X1, X2) = (5, -5) + a(0, 1) = (5, -5 + a), for a > 0.
The derivative of f(X) with respect to a is:
f ‘ (a) = å ¶ f(X) / ¶Xi . ¶Xi / ¶a = 5(0) + (-2X2 + 4)(1) = 14 - 2a, for a > 0.
The derivative vanishes at a = 7, therefore a critical point is at (5, 2), with the objective function value of 9. Since f'(a) is positive for any a > 7 , therefore the objective function is increasing beyond this point, hence, there is no global maximum point for this problem.
Step 4: Evaluation of Objective Function at the Vertices of the Feasible Region:
| X1 | X2 | f(X) | ||
| ___________________ | ||||
| 0 | -30 | -1020 | ||
| 5 | -5 | -40 | ||
Therefore, the global optimal solution is: X1 = 0, and X2 = -30, with optimal value = -1020.
Post-optimality Analysis:
Sensitivity Analysis and Its Applications
Tolerance analysis by Wendel (1984, 1985) is a special case of general post-solution analysis; e.g., Bonnans, and Shapiro (2000), and Arsham (1990). Tolerance analysis deals with simultaneous and independent equal changes expressed as maximum allowable percentage of the parameters’ value in both directions (over and under estimation) for all parameters that maintain the optimal solution structure. This provides one single range of values of uncertainty for all parameters. This type of analysis is widely used in LP models; e.g., Arsham (1990). An interesting approach for handling uncertainties with LP modeling parameters is presented in Chen, and Huang (2001). An extension of the tolerance analysis to convex quadratic programs is given in Gupta and Bhatia (2000).
The following is an extension of the tolerance analysis to nonlinear programs in the context of the previous numerical example from Kaul, et al. (1999).
Consider the following (nominal) problem from et al. (1999), which is solved by the Karush-Kuhn-Tucker conditions therein.
Step 1: Finding the Interior Critical Points: The gradient of the objective function is (-1 + X1 - X2, -1 - X1 + 2X2). The gradient vanishes at point G = (3, 2) with objective function value –2.5, which is not feasible, since it does not satisfy the first constraint. Therefore, there is no interior critical point.
Step 2: Finding the Vertices of the Feasible Region: The three vertices of the feasible region are A (3, 0), B = (0, 3), and C = (0, 2), which can be verified by the graphical method for this two-dimensional problem. The objective function is then evaluated at each vertex:
f(A) = f(3, 0) = 3/2, f(B) = f(0, 3) = 6, and f(C) = f(0, 2) = 2,
Step 3: Finding the Critical Points on the Boundary Line Segments: Parametric representation of the gradient of the objective function, using the convex combination of the two vertices for every boundary line segment, enables us to find the boundary critical point. For example, to find any critical point on line segment AB, we first construct the parametric version of this line segment as:
| X1 = 3l1 + 0l2 = 3l1 |
| X2 = 0l1 + 3l2 = 3(1 - l1) = 3 - 3l1 |
Using the chain-rule, the derivative of f(l2) with respect to l1 is:
f ‘ (l1) = å ¶ f(X) / ¶Xi . ¶Xi / ¶l1 =
= (-1 + X1 - X2)(3) + (-1 - X1 + 2X2)(-3)
= 6X1 - 9X2 = 45l1 – 27, over the open set 0 <l2< 1
The derivative vanishes at l1 = 3/5. This gives a boundary critical point C1 = (X1 = 3l1 = 9/5, X2 = 3 - 3l1 = 6/5) with objective values of -21/10 = -2.1.
There is no critical point on the boundary line BC. However, there is a critical point C2 on the line segment AC at (X1 = 45/29, X2 = 28/29) with objective values of -109/58 = -1.879.
Step 4: Comparing the numerical values of f(X) at the critical points and the vertices, we conclude that the global minimum point is at point C1 = (9/5, 6/5) with global optimal value of -2.1.
Therefore, one readily constructs the numerical tight bounds for the objective function, that is,
-2.1 £ X12/2 + X22 - X1X2 - X1 - X2
£ 6, over its feasible region.
Now consider the above nominal numerical example with the following RHS perturbation:
In order to maintain the current optimal solution structure, we perform the same process as before; however, we carry the perturbed parameter a. To maintain the general structure of the feasible region, it is clear that it is empty for a < -1. However, for a = -1, the feasible region consists of single point (0, 0). Therefore, we impose the condition that a > -1. Under this condition, the polytope has the perturbed vertices: A = (3 + 3a, 0), B = (0, 3 + 3a ) and C = (0, 2 + 2a).
Since the objective function has global minimum at G = (3,2), we first have to find out for which values of parameter a this point becomes feasible. It is easy to see that G is feasible for 2/3 £ a £ 1. It means that, for 2/3 £ a £ 1, the critical point at the edge AB is no longer optimal, but the optimal solution is the point G.
Since the aim of tolerance analysis is to find out for which values the current critical parametric point C1 remains optimal, we have to perform the same process as before with the perturbed vertices. We find the perturbed critical points C1 = [9/5(1 +a), 6/5(1 +a)] on the edge AB and C2 = [(42a + 45)/29, (30a + 28)/29] on the edge AC. The values of objective function at both critical points and vertices are:
- f(A) = 9/2a2 + 6a + 3/2
- f(B) = 9a2 + 15a + 6
- f(C) = 4a2 + 6a + 2
- f(C1) = 9/10a2 – 6/5a – 21/10
- f(C2) = 18/29a2 – 36/29a – 109/58
It can be shown that:
- f(C1) < f(A) for every a ¹ -1,
- f(C1) < f(B) for every a ¹ -1,
- f(C1) < f(C) for every a > -1,
We only have to find out for which values of a the inequality f(C1) < f(C2) holds. By solving
9/10a2 – 6/5a – 21/10 < 18/29a2 – 36/29a – 109/58,
we find out that f(C1) < f(C2) for [-2 - 2(145)1/2]/27 < a < [-2 + 2(145)1/2] / 27 or -0.966 < a < 0.818.
Now we can conclude that the optimal solution is:
- at the point G for 2/3 £ a £ 1,
- at the point C1 for [-2 - 2(145)1/2] / 27 £ a £ 2/3, and
- at the point C2 for a ³ 1 and –1 < a £ [-2 - 2(145)1/2] / 27
Therefore, critical point C1 remains optimal as long as [-2 - 2(145)1/2] / 27 £ a £ 2/3. Therefore, the symmetric tolerance limits are -2/3 £ a £ 2/3. The obtained tolerance factor provides larger tolerance bound (66%) than the 19% found by the above reference.
Concluding Remarks
In the proposed solution we needed to find all the critical points. However, since the gradient of a function is always defined on an open domain. Therefore, we solved a series of unconstrained problems. First, we identify the vertices and the extreme rays (if any) of the feasible region. Then, we found critical points on the interior points of the feasible region. Next, we found critical points on interior points of the faces of the feasible region, then on interior points of the edges (i.e., line segments) of the feasible region. Finally, by functional evaluation of the objective function at the critical points and the vertices of the feasible region the global optimal solution was found. The parametric representation was extended to optimization over polyhedrons.
The algorithmic strategy can be stated quite simply as finding all the critical points of the parametric objective function over the feasible region via representation of the feasible region as a convex combination of its vertices.
While all the derivative based algorithms such as Lagrange and KKT methods give local points, the proposed solution algorithms provides the global solution. Notice also that, the Lagrange and KKT and (penality-based) methods "appear" to remove the constraints by using a linear (or non-linear) combination of the constraints in a penalty function, the proposed solution algorithm, however, uses the linear convex combination of vertices to remove the constraints.
It favorably compares with other methods for this type of problems. The proposed algorithm has simplicity, potential for wide adaptation, and deals with all cases. However, this does not imply that all distinction among problems should be ignored. One must incorporate the special characteristic of the problem to modify the proposed algorithm in solving them.
The approach presented in this paper is also a good tutorial, since it can be presented as a natural bridge from the graphical method to the simplex method in solving LP problems, as well as advanced techniques for solving general nonlinear programs.
The proposed solution algorithm has nice features:
- It should prove useful for an introduction to mathematical programming before introducing more advanced topics.
- It is a general purpose solution algorithm, that is, one treatment for all linearly constraints optimization problems with continuous objective functions.
- Unlike other general purpose solution methods, such as KKT conditions, it guarantees global optimal solution.
- It is intuitively simple to be understood by non-mathematical major students and the managers.
- It is relatively easy to implement.
- It provides useful information such all critical points which in turn, provides upper and lower tight bounds on the objective function over the feasible region.
- It provides useful managerial information such as sensitivity analysis and its applications to tolerance analysis.
- Since, there are many optimization problems with simply given postulated known solutions [see, e.g., Pardalos P., and Rosen J. (1987)], the proposed solution algorithm is an effective tool for both, verifying the postulated known solutions or finding the best solution(s).
Linear dependence among the linear constraints is commonplace in practical problems. Linear dependence among linear constraints that are binding at a point is commonly known as degeneracy and such a point is called a degenerate point. The resolution of degeneracy at a vertex is essentially a combinatorial problem whose solution may require a significant amount of computation, see, e.g., Gill et. al. (1989). Since our approach is an explicit enumeration technique as opposed to a path- following methods, it is free from computational problems that may be caused by degeneracy.
Since the solution algorithm is a general purpose, therefore there is always room for some effective modifications for any specific class of problems. Some areas for future research include development of possible refinements such as, decomposition by way of not the convex combination of all vertices, but some, say k, k > n + 1. An immediate work is development of an efficient computer code to implement the approach, and performing a comparative computational study. A convincing evaluation for the reader would be the application of this approach to a problem he/she has solved by any other method as we did this in this paper.
References
Altherr W. (1975). An algorithm for enumerating the vertices of a convex polyhedron, Computing, 15, 181-193.
Arsham H. (2005). Tight bounding of continuous functions over polyhedrons: A new introduction to exact global optimization, International Journal of Pure and Applied Mathematics, 19(3), 393-413.
Arsham H. (2004). Global optima for linearly constrained business decision models, Scientific Journal of Administrative Development, 2(1), 27-53.
Arsham H. (1997a). Affine geometric method for linear programs, Journal of Scientific Computing, 12, 289-303.
Arsham H. (1997b). Initialization of the simplex algorithm: An artificial-free approach, SIAM Review, 39, 736-744.
Arsham H. (1999). Computational geometry and linear programs, International Journal of Mathematical Algorithms, Formerly, International Journal of Mathematical Algorithms, 1, 251-266.
Arsham H. (1997). An artificial-free simplex algorithm for general LP models, Mathematical and Computer Modelling, 25, 107-123.
Arsham H. (1999). Stability analysis of the critical path in project activity networks, Civil Engineering and Environmental Systems, 15, 305-334.
Arsham H. (1998). Distribution-routes stability analysis of the transportation problem, Optimization, 43, 47-72.
Arsham H. (1998). Managing cost uncertainties in transportation and assignment problems, Journal of Applied Mathematics & Decision Sciences, 2, 65-102.
Arsham H. (1992). Postoptimality analysis for the transportation problem, Journal of the Operational Research Society, 43, 121-139.
Arsham H. (1990). A complete algorithm for linear fractional programs, Computers & Mathematics with Applications, 20, 11-23.
Arsham H. (2004). Global optima for linearly constrained business decision models,
Scientific Journal of Administrative Development, 2(1), 27 – 53.
Arsham, H. (1990), Perturbation analysis of general LP models: A unified approach to sensitivity, parametric tolerance, and more-for-less analysis, Mathematical and Computer Modelling, 12 (1), 79-102.
Arsham H. (2003). Globally tight bounds for almost differentiable functions over polytopes with application to tolerance analysis, OPSEARCH: Journal of the Operational Research Society of India, 40(4), 305-319.
Arsham H. (1995). A comprehensive simplex-like algorithm for network optimization and perturbation analysis, Optimization, 32, 211-267.
Arsham H. (1998). Managing cost uncertainties in transportation and assignment problems, Journal of Applied Mathematics & Decision Sciences, 2 (1), 65-102.
Arsham H. (1993). Managing project activity-duration uncertainties, Omega: International Journal of Management Science, Volume 21, (2), pp. 111-122.
Arsham H., et al. (2002). Continuous global optimization over polyhedrons: A new introduction to optimization, International Mathematical Journal, 1(1), 37-52.
Arsham H., et al. (2003). Linearly constrained global optimization: A general solution algorithm with applications, Applied Mathematics and Computation, 134(2-3), 345-361, 2003.
Arsham H., and Štemberger M. (2003). From linear to nonlinear optimization: The missing chapter,
Journal of Mathematical Education in Science & Technology, 34(3), 417-430.
Avis D., and Fukuda, K. (1992). A pivoting algorithm for convex hulls and vertex enumeration of arrangements and polyhedra, Discrete and Computational Geometry, 8 (4), 295-313.
Avis D., Bremner, D. and Seidel R. (1997). How good are convex hull algorithms?, Computational Geometry: Theory and Applications, 7(5), 265-301.
Barrientos O., and Correa R. (2000). An algorithm for global minimization of linearly constrained quadratic functions, Journal of Global Optimization, Volume 16, (1), pp. 77-93.
Best M., and Caron R. (1985). The simplex method and unrestricted variables, Journal of Optimization Theory and Applications, 45, 33-39.
Bonnans J., and Shapiro, A. (2000). Perturbation Analysis of Optimization Problems, Springer, New York.
Boot J., (1964). Quadratic Programming: Algorithms: Anomalies and Applications, North-Holland Publ.
Boyd S., and L. Vandenberghe, (2004). Convex Optimization, Cambridge University Press.
Bremner D, Fukuda K and Marzetta A. (1997). Primal-dual methods for vertex and facet enumeration. In the Proceedings of the 13th Annual ACM Symposium on Computer Geometry, 49-56.
Chadha S. (1999). A linear fractional program with homogenous constraints, Opsearch, 36(4), 390-398.
Chen M., and Huang G. (2001). A derivative algorithm for inexact quadratic program: Application to environmental decision-making under uncertainty, European Journal of Operational Research, 128 (3), 570-586.
Chen X., and M. Fukushima. (1999). Proximal quasi-Newton methods for nondifferentiable convex optimization, Mathematical Programming, 85A, 313-334.
Chvatal V., Linear Programming, W. H. Freeman and Company, New York (1983).
Corradi G., (2001). Higher-order derivatives in linear and quadratic programming, Computers and Operations Research, 28, 209-222.
Craven B., and S. Islam, Optimization in Economics and Finance, Springer , 2005.
Deuflhard P., Newton Methods for Nonlinear Problems: Affine Invariance and Adaptive Algorithms, Springer, 2004.
Dravnieks E., and J. Chinneck (1997). Formulation assistance for global optimization problems, Computers & Operations Research 24, 1157-1168.
Elton E., Gruber, M., Brown S., and Goetzman, W. (2003). Modern Portfolio Theory and Investment Analysis, John Wiley and Sons, Inc., New York, pp. 182-208.
Fiacco A., and G. McCormick (1990). Nonlinear Programming: Sequential Unconstrained Minimization Techniques, Classics in Applied Mathematics, 4, SIAM, Philadelphia, PA.
Fletcher R. (1987). Practical Methods of Optimization, Wiley, New York.
Fukuda K., T. Liebling, and F. Margot (1997). Analysis of backtrack algorithms for listing all vertices and all faces of a convex polyhedron, Computational Geometry: Theory and Applications, 8, 1-12.
Fukuda K., and Rosta, V. (1994). Combinatorial face enumeration in convex polytopes, Computational Geometry, 4 (1), 191-198.
Gill P., W. Murray, Saunders M. and M. Wright, (1989). A practical anti-cycling procedure for linearly constrained optimization, Mathematical Programming: Series B, 45(3), 437-474.
Grinold R., and R. Kahn, (1995). Active Portfolio Management, Probus Publishing, Chicago.
Gupta P., and Bhatia D. (2000). Multiparametric analysis of the maximum tolerance in quadratic programming problems, Operations Research, 37 (1), 36-46.
Haugen R. (1997). Modern Investment Theory, Prentice Hall, Upper Saddle River, New Jersey, 92-130.
Hillier F., and G. Lieberman (1995). Introduction To Operations Research, McGraw-Hill Co., New York, NY.
Hiriart-Urruty J. (1998). Conditions for global optimality, Journal of Global Optimization, Volume 13(3), 349-367.
Horst R., Nast M., and Thoai N. (1995). New LP-bound in multivariate Lipschitz optimization: theory and applications, Journal of Optimization Theory and Applications, 86(2), 369-388.
Horst R., and Tuy H. (1996). Global Optimization, Deterministic Approaches, Springer, Berlin.
Ibidapo-Obe O., O. Asaolu, and A. Badiru, (2002), A new method for the numerical solution of simultaneous nonlinear equations, Applied Mathematics and Computation, 125(1), 133-140.
Kalantari B. (1985). Construction of difficult linearly constrained concave minimization problems, Operations Research, 33 (1), 222-227.
Kallio M, and S. Salo, (2000). An interior point method for solving systems of linear equations and
inequalities, Operations Research Letters, 27, 101-107.
Kaul R. Bhatia, D., and Gupta P. (1999). Tolerance approach to sensitivity analysis in quadratic programs, Opsearch, 36 (1), 1-9.
Kelley C. (1995). Iterative Methods for Linear and Nonlinear Equations, SIAM, Philadelphia, PA.
Kreps D. (1990). A Course in Microeconomic Theory, Princeton University Press, New Jersey.
Kritzman M., (1995). The Portable Financial Analyst: What Practitioners Need to Know, Probus Publishing, Chicago.
Kucherenko S., and Sytsko Y. (2005). Application of deterministic low-discrepancy sequences in global optimization, Computational Optimization and Applications, 30(3), 297-318. A Monte Carlo (random search) approach to global optimixation.
Le-An T., and Tao P. (1997). Solving a class of linearly constrained indefinite quadratic problems by D.C. algorithms, Journal of Global Optimization, 11 (3), 253-285.
Markland R. and Sweigart J. (1987). Quantitative Methods: Applications to Managerial Decision Making, John Wiley & Sons, New York.
Markowitz H., (1959). Portfolio Selection Efficient Diversification of Investments, John Wiley and Sons, New York.
Martin R., (1999). Large Scale Linear and Integer Optimization: A Unified Approach, Kluwer Academic Publishers.
Matheiss T., and D. Rubin, (1980). A survey and comparison of methods for finding all vertices of convex polyhedral sets, Math. Oper. Res., 5, 167-185.
Mijangos E., and N. Nabona, (2001). On the first-order estimation of multipliers from Kuhn-Tucker systems, Computers and Operations Research, 28, 243-270.
Nocedal J., and S. Wright, (2006). Numerical Optimization, Springer.
Pardalos P., and Rosen J. (1987). Constrained Global Optimization: Algorithms and Applications, Lecture Notes in Computer Science, Springer, Berlin.
Pardalos P., and Schnitger G. (1987). Checking local optimality in constrained quadratic programming is NP-hard. Technical Report, Computer Science Department, The Penn. State University, Pennsylvania.
Pintér J., (1999). Continuous Global Optimization: An Introduction to Models, Solution Approaches, Tests and Applications, 2, ITORMS.
Pinter J. (1996). Global Optimization in Action: Continuous and Lipschitz Optimization: Algorithms, Implementations and Applications, Kluwer Academic Publishers, UK.
Roos C., T. Terlaky, and J. Vial, (1997). Theory and Algorithms for Linear Optimization: An Interior Point Approach, Wiley, UK.
Rudin W. (1976). Principles of Mathematical Analysis, McGraw-Hill, New York.
Schrijver A. (2003), Combinatorial Optimization: Polyhedra and Efficiency, Springer Verlag.
Sharpe W., Alexander G., and Bailey J. (1999). Investments, Prentice Hall, Upper Saddle River, New Jersey, pp. 193-200.
Sinha S., and Tuteja, G. (1999). On fractional programming, Opsearch, 36 (6), 418-424.
Sherali H., Choi G., and C. Tuncbilek, (2000). A variable target value method for nondifferentiable optimization, Operations Research Letters, 26, 1-8.
Steinbach M., (2001). Markowitz revisited: mean-variance models in financial portfolio analysis. SIAM Review, 43, 31-85.
Software for System of Inequalities
Townsend E., Functions of Real Variables, H. Holt and Company, New York, 1928. pp. 385-386.
Thi H., D. Pham, and Thoai N. (2002). Combination between global and local methods for solving an optimization problem over the efficient set, European Journal of Operational Research, 142, (2), 258-270.
Tuteja G., (2000). Programming with the sum of linear and quotient objective function, Opsearch, 37 (2), 177-180.
Von Hohenbalken B. (1977). Simplicial decomposition in nonlinear programming algorithms, Mathematical Programming, 13, 49-68.
Wendel R. (1984). Using bounds on the data in linear programming: The tolerance approach to sensitivity analysis, Mathematical Programming, 29 (2), 304-322.
Wendel R. (1985). The tolerance approach to sensitivity analysis in linear programming, Management Science, 31(4), 517-523.
Williams H., (1993). Model Solving in Mathematical Programming, Wiley, Chichester, UK.
Winston W. (1997). Introduction to Mathematical Programming: Applications and Algorithms, Wadsworth Pub Co., New York, NY.
Yamada T, Yoruzuya J, and Kataoka (1994). Enumerating extreme points of a highly degenerate polytope, Computers & Operations Research, 21, 397-410.
Yamashita H., and H. Yabe (2005), Quadratic convergence of a primal-dual interior point method for degenerate nonlinear optimization problems, Computational Optimization and Applications, 31(2), 123-144.
Ziegler G. (1995). Lectures on Polytopes, Springer-Verlag, New York.
Optimization Modeling Process: Linear Programming
main Web site.
The Copyright Statement: The fair use, according to the 1996 Fair Use Guidelines for Educational Multimedia, of materials presented on this Web site is permitted for non-commercial and classroom purposes only.
This site may be mirrored intact (including these notices), on any server with public access, and linked to other Web pages. All files are available at http://home.ubalt.edu/ntsbarsh/Business-stat for mirroring.
Kindly e-mail me your comments, suggestions, and concerns. Thank you.
This site was launched on 4/25/1998, and its intellectual materials have been thoroughly revised on a yearly basis. All external links are checked once a month.
EOF: Ó 1998-2015.